LLVM 循环术语

循环

循环是 LLVM 循环的推广，定义如下 [HavlakCycles]

  1. 在有向图 G（函数 CFG 或其子图）中，循环是一个最大强连通区域，至少包含一条内部边。（信息性注释 — 至少一条内部边的要求确保只有当存在返回同一基本块的边时，单个基本块才是一个循环。）

  2. 循环中的一个基本块，如果可以从函数入口沿不访问循环中任何其他基本块的路径到达，则称为该循环的入口。一个循环可以有多个入口。

  3. 对于从函数入口开始的给定深度优先搜索，循环中第一个被访问的节点称为该循环的头，相对于特定的 DFS。头始终是一个入口节点。

  4. 在从入口开始的任何深度优先搜索中，在 CFG 中找到的循环集合是相同的。这些是不具有父级的顶层循环。

  5. 嵌套在头为 H 的循环 C 内的子循环（或简称循环）是在节点集合 (C - H) 上导出的子图中的循环。C 被称为这些循环的父循环。

因此，循环形成一个实现定义的森林，其中每个循环 C 是嵌套在 C 内的任何子循环的父循环。该树紧密地遵循同一函数中循环的嵌套。可约循环（LLVM 循环）L 的唯一入口支配其所有其他节点，并且无论使用何种 DFS 树，始终被选为某个循环 C 的头。此循环 C 是循环 L 的超集。对于不可约循环，没有一个入口支配循环的节点。其中一个入口以实现定义的方式被选为循环的头。

如果一个循环有多个入口，则它是不可约的，否则是可约的。

如果基本块 B 出现在循环 C 中，但未出现在 C 的任何子循环中，则称循环 C 是基本块 B 的父循环。然后 B 也被称为循环 C 的子循环。

如果块 B 不是任何循环的子循环，则称块 B 为顶层块。

如果基本块或循环 X 和另一个基本块或循环 Y 都无父循环，或者都有相同的父循环，则它们互为兄弟。

信息性注释

  • 循环的非头入口块可以包含在子循环中。

  • 如果 CFG 是可约的，则循环恰好是自然循环，并且每个循环都只有一个入口块。

  • 循环是良好嵌套的（根据定义）。

  • 循环的入口块在支配树中是兄弟节点。

[HavlakCycles]

Paul Havlak，“可约和不可约循环的嵌套。” ACM 编程语言和系统事务 (TOPLAS) 19.4 (1997): 557-567。

循环示例

包含自然循环的不可约循环

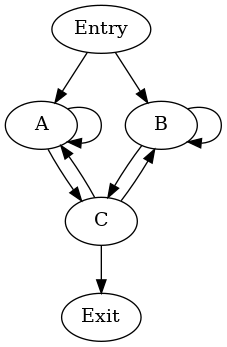
_images/cycle-1.png

A 和 B 的自循环产生两个单块自然循环。可能的循环层次结构是

cycle: {A, B, C} entries: {A, B} header: A
- cycle: {B, C}  entries: {B, C} header: C
  - cycle: {B}   entries: {B}    header: B

当 DFS 以 A、C、B 的顺序（前序）访问块时，会出现这种层次结构。

两个自然循环的不可约并集

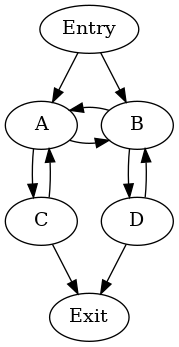
_images/cycle-2.png

存在两个自然循环：{A, C} 和 {B, D}。可能的循环层次结构是

cycle: {A, B, C, D} entries: {A, B} header: A
- cycle: {B, D}     entries: {B}    header: B

不包含自然循环的不可约循环

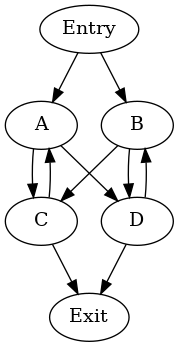
_images/cycle-3.png

此图不包含任何自然循环 — 节点 A、B、C 和 D 在支配树中是兄弟节点。可能的循环层次结构是

cycle: {A, B, C, D} entries: {A, B} header: A
- cycle: {B, D}     entries: {B, D} header: D

闭合路径和循环

CFG 中的闭合路径是 CFG 中节点和边的连接序列，其开始和结束节点相同，并且其余（内部）节点是不同的。

闭合路径 P 的入口是 P 上的一个节点，可以从函数入口到达，而无需通过 P 上的任何其他节点。

  1. 如果节点 D 支配闭合路径 P 中的一个或多个节点，并且 P 不包含 D，则 D 支配 P 中的每个节点。

    证明： 设 U 是 P 中被 D 支配的节点。如果 P 中存在未被 D 支配的节点 V，那么 U 将可以通过 V 从函数入口节点到达，而无需通过 D，这与 D 支配 U 的事实相矛盾。

  2. 如果节点 D 支配闭合路径 P 中的一个或多个节点，并且 P 不包含 D，则存在一个包含 P 但不包含 D 的循环 C。

    证明： 从上述性质可知，D 支配 P 中的所有节点。对于实现定义的 DFS 发现的任何循环嵌套，考虑包含 P 的最小循环 C。为了反证，假设 D 在 C 中。那么 C 的头 H 不能在 P 中，因为循环的头不能被循环中的任何其他节点支配。因此，P 在集合 (C-H) 中，并且在 C 中必须存在一个也包含 P 的较小循环 C'，但这与我们选择 C 的方式相矛盾。

  3. 如果闭合路径 P 包含节点 U1 和 U2，但不包含它们各自的支配节点 D1 和 D2，则存在一个循环 C，它包含 U1 和 U2，但不包含 D1 和 D2。

    证明： 从上述性质可知，D1 和 D2 分别支配 P 中的每个节点。存在一个循环 C1（分别为 C2），它包含 P，但不包含 D1（分别为 D2）。C1 和 C2 要么是同一个循环，要么其中一个嵌套在另一个内部。因此，总存在一个循环，它包含 U1 和 U2，但不包含 D1 和 D2。

  1. 在任何循环层次结构中，包含闭合路径 P 的最小循环 C 的头 H 本身位于 P 上。

    证明： 如果 H 不在 P 中，则在集合 C - H 中存在一个包含 P 的较小循环 C'，这与 C 是最小此类循环的说法相矛盾。

可约循环头

尽管循环层次结构取决于选择的 DFS，但可约循环满足以下不变性

如果在任何 DFS 中发现头为 H 的可约循环 C，则在每个 DFS 中都存在一个头为 H 的循环 C'，它包含 C。

证明： 对于 C 中通过 H 的闭合路径 P，每个循环层次结构都有一个包含 P 的最小循环 C'，并且其头在 P 中。由于 H 是 P 的唯一入口，因此 H 必须是 C' 的头。由于头唯一地定义循环，因此 C' 包含每个这样的闭合路径 P，因此 C' 包含 C。